自动控制复习

一、知识点

1. 衡量或评价控制系统优劣的三个方面

   • 稳定性
   • 快速性
   • 准确性

2. 自动控制系统的基本控制方式可以分为哪些

   • 开环控制
   • 闭环控制

3. 线性定常离散控制系统的稳定性，除了与系统的结构参数有关之外，还与什么因素有关

   • 采样周期

4. 根轨迹上的点应该同时满足什么条件

   • 相角条件
   • 幅值条件

5. 根轨迹起始于什么，终止于什么

   • 起始于开环极点

   • 终止于开环零点

6. 线性连续系统的稳态误差，除了与系统结构参数有关之外，还与什么有关

   • 输入信号

7. 离散系统脉冲传递函数G(z)的定义是什么

   • 是在零初始条件下，C(z)比上R(z)

   • \(G(z)=\frac{C(z)}{P(z)}\)

8. 连续系统稳定的充分必要条件是什么

   • 所有的闭环特征根具有负实部

9. 在频率特性法中，采用什么来衡量系统的相对稳定性

   • 幅值预料
   • 相角预料

10. 传递函数反映的是什么

    • 单输入，单输出线性定常系统在零初始条件下的动态特性

11. 惯性环节在转折频率处的模值为，相角为

    • \(模值为 \frac{\sqrt{2}}{2}\)

    • \(相角为 -45^{\circ}\)

12. 奈奎斯特稳定判据中，Z=P-2N，其中Z代表什么，P代表什么，N代表什么

    • Z：闭环特征根在X右半平面的个数
    • P：开环极点在X右半平面的个数
    • N：开环幅相曲线穿越-1之左实轴的次数

13. 稳定的线性定常系统在谐波输入下，输出的稳态分量仍然是与输入同频率的谐波函数，而幅值和相位的变化是频率ω的函数，请问频率特性的表达式怎么写，并说明频率特性、幅频特性和相频特性的定义

    • \(幅频特性 A(w)=\vert G(j w)\vert\)

    • \(相频特性 A(w)=\angle G(J w)\)

    • \(频率特性 A(w) e^{j φ^{(\omega)}}=\vert G(j w)\vert e^{jG(j w)}=G(j w)=\left.G(s)\right\vert_{s=j w}\)

14. 简述频率特性的定义，并说明稳定的线性定常系统在谐波输入下输出响应与输入频率的关系

    • 当线性系统的输入端加上一频率为ω的正弦信号时，系统的稳态输入是与输出同频率的正弦信号，其幅值和相位是频率ω的函数
    • \(或用公式表示 C_{s}(t)=A\vert G(j w)\vert \sin [w t+(G(j w)]\)

15. 已知某二阶系统的闭环传递函数\(\varphi(s)=\frac{4}{s^{2}+2 s+4}\)，求谐振频率\(\omega_{r}\)和谐振峰值\(M_{r}\)

    • 谐振频率 \(\omega_{r}=\omega_{n} \sqrt{1-2 \xi^{2}} \qquad (0 \leq \xi \leq 0.707)\)

    • 谐振峰值 \(M_{r}=\frac{1}{2 \xi \sqrt{1-\xi^{2}}}\)

16. 闭环系统\(\varphi(s)=\frac{4}{s+2}\)，如果输入信号为阶跃信号，求输出响应的调节时间

• 一阶系统的调节时间为3T

• T为将分母常数项化为一，S前面的参数，本题为\(\frac{1}{2}\)

• 调节时间为\(\frac{3}{2}\)

17. 闭环系统\(\varphi(s)=\frac{4}{s+2}\)，如果输入信号为正弦信号\(\sin (2 t)\)，求稳态输出

    • 套用公式 \(C_{s}(t)=A\vert G(j w)\vert \sin [w t+(G(j w)]\)

18. 已知某系统的开环传递函数\(G(s)=\frac{5}{s(s+2)}\)，问它的型别和开环增益

    • 型别：开环传递函数分母在原点处的极点个数，本题中为1，因此是1型
    • 开环增益：去掉型别（s），常数项化为1，剩下的S取0，得到开环增益为\(\frac{5}{2}\)

19. 已知某单位反馈系统，误差传递函数为\(\varphi_{e r}(s)=\frac{s+1}{s+2}\)，当输入为\(\sin (2 t)\)时，求稳态误差

    • 套用公式 \(C_{s}(t)=A\vert G(j w)\vert \sin [w t+(G(j w)]\)

二、计算题

1、（2-7）求系统的传递函数C(s)，E(s)。

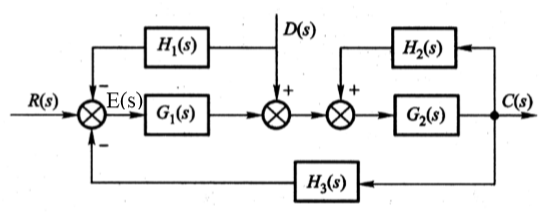
解：

$L_{1}=-G_{1} G_{2} H_{3} $

$L_{2}=G_{2} H_{2} $

$R(s) C(s): P_{1}=G_{1} G_{2}, _{1}=1 $

\(\frac{C(S)}{R(S)}=\frac{G_{1} G_{2}}{1+G_{1} G_{2} H_{3}-G_{2} H_{2}}\)

$D(s) C(s): P_{1}=G_{2}, {1}=1 ,P{2}=-G_{1} G_{2}H_{1}, _{2}=1 $

\(\frac{C(s)}{D(s)}=\frac{G_{2}-G_{1} G_{2} H_{1}}{1+G_{1} G_{2} H_{3}-G_{2} H_{2}}\)

总输出为：

\(C(s)=\frac{G_{1} G_{2}}{1+G_{1} G_{2} H_{3}-G_{2} H_{2}} \cdot R(s)+\frac{G_{2}-G_{1} G_{2} H_{1}}{1+G_{1} G_{2} H_{3}-G_{2} H_{2}} \cdot D(s)\)

（2） $R(s) E(s): P_{1}=1, {1}=1-G{2} H_{2} \ = $

$D(s) E(s): P_{1}=-G_{2} H_{3}, {1}=1, P{2}=-H_{1}, {2}=1-G{2} H_{2} $

\(\frac{E(s)}{D(s)}=\frac{-G_{2} H_{3}-H_{1}\left(1-G_{2} H_{2}\right)}{1+G_{1} G_{2} H_{3}-G_{2} H_{2}}\)

总误差为：

\(E(s)=\frac{1-G_{2} H_{2}}{1+G_{1} G_{2} H_{3}-G_{2} H_{2}} \cdot R(s)+\frac{-G_{2} H_{3}-H_{1}\left(1-G_{2} H_{2}\right)}{1+G_{1} G_{2} H_{3}-G_{2} H_{2}} \cdot D(s)\)

2、（2-8）试求图示系统中的 C(s)

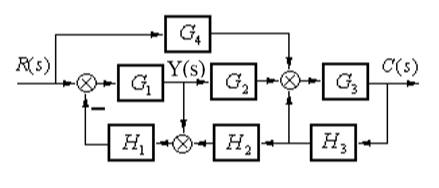
解：

\(L_{1}=-G_{1} H_{1}\)

\(L_{2}=-G_{1} G_{2} G_{3} H_{1} H_{2} H_{3}\)

\(L_{3}=G_{3} H_{3}\)

\(L_{1} L_{3}=\left(-G_{1} H_{1}\right)\left(G_{3} H_{3}\right)\)

\(R(s) \rightarrow C(s): P_{1}=G_{1} G_{2} G_{3}, \Delta_{1}=1; P_{2}=G_{14} G_{3}, \Delta_{1}=1-(-G_{1} H_{1})\)

\(\frac{C(s)}{R(s)}=\frac{G_{1} G_{2} G_{3}+G_{4} G_{3}\left[1-\left(-G_{1} H_{1}\right)\right]}{1-\left(-G_{1} H_{1}\right)-\left(-G_{1} G_{2} G_{3} H_{1} H_{2} H_{3}\right)-\left(G_{3} H_{3}\right)-\left(-G_{1} H_{1}\right)\left(G_{3} H_{3}\right)}\)

\(Y(s) \rightarrow C(s): P_{1}=G_{2} G_{3}, \Delta_{1}=1-(-G_{1} H_{1})\)

\(\frac{C(s)}{Y(s)}=\frac{G_{2} G_{3}\left[1-\left(-G_{1} H_{1}\right)\right]}{1-\left(-G_{1} H_{1}\right)-\left(-G_{1} G_{2} G_{3} H_{1} H_{2} H_{3}\right)-\left(G_{3} H_{3}\right)-\left(-G_{1} H_{1}\right)\left(G_{3} H_{3}\right)}\)

总输出为：

\({C(s)}=\frac{G_{1} G_{2} G_{3}+G_{4} G_{3}\left(1+G_{1} H_{1}\right)}{1+G_{1}H_{1}+G_{1} G_{2} G_{3} H_{1} H_{2} H_{3}-G_{3} H_{3}+G_{1} G_{3} H_{1} H_{3}} \cdot R(s) \\+ \frac{G_{2} G_{3}\left(1+G_{1} H_{1}\right)}{1+G_{1}H_{1}+G_{1} G_{2} G_{3} H_{1} H_{2} H_{3}-G_{3} H_{3}+G_{1} G_{3} H_{1} H_{3}} \cdot R(s)\)

3、（7-9）设离散系统如图所示，其中 T=0.1s，K=1，求

1. 系统的闭环脉冲传递函数；
2. 判断系统的稳定性；
3. 系统在r(t)=t作用下的稳态误差\(e^{*}(\infty)\)；

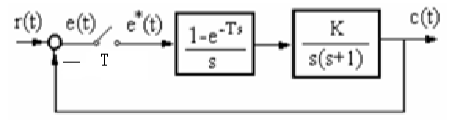
解：

​ 系统的开环脉冲传递函数为： \(G(z)=\left(1-z^{-1}\right) Z\left[\frac{1}{s^{2}(s+1)}\right]=\left(1-z^{-1}\right)\left[\frac{T z}{(z-1)^{2}}-\frac{\left(1-e^{-T}\right) z}{(z-1)\left(z-e^{-T}\right)}\right]\)

​ 将T=0.1带入并整理得\(G(z)=\frac{0.005(z+0.9)}{(z-1)(z-0.905)}\)，

\(K_{p}=\lim _{x \rightarrow 1}[1+G(z)]=\lim _{x \rightarrow 1}\left[1+\frac{0.005(z+0.9)}{(z-1)(z-0.905)}\right]=\infty\)

\(K_{v}=\lim _{z \rightarrow 1}(z-1) G(z)=\lim _{z \rightarrow 1}(z-1) \frac{0.005(z+0.9)}{(z-1)(z-0.905)}=0.1\)

\(e(\infty)=\frac{T}{K_{v}}=1\)

4、（7-8）设离散系统如图所示，采样周期T=1s，\(G_{h}(s)\)为零阶保持器，而\(G(s)=\frac{K}{s+1}\)，求：

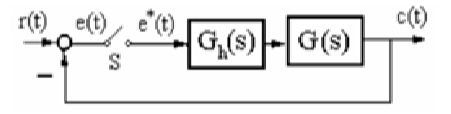
1. 确定使系统稳定的K的范围
2. 设K=2，求系统在阶跃信号作用下的稳态误差

解：

思路：\(G(z) \Rightarrow \phi(z) \Rightarrow D(z)=0 \quad \Rightarrow\left\vert z_{i}\right\vert <1\)

（1）

5、（4-4）控制系统的开环传递函数为\(G(s)=\frac{K_{r}}{s(s+2)(s+4)}\)，求：

1. 绘制根轨迹图（写出5个步骤）
   1. 开环零、极点
   2. 实轴上的根轨迹段
   3. 根轨迹的渐近线、夹角
   4. 分离点
   5. 与虚轴的交点
2. 判断系统临界稳定的\(K_{r}\)，并求等幅振荡的频率

解：

（1）

开环零点、极点：\(P_{1}=0，P_{1}=-2，P_{3}=-4，n=3\)

实轴上的根轨迹段：（0，-2）（-4，-\(\infty\)）

渐近线交点及夹角：

\(\sigma_{a}=\frac{0-2-4}{3}=-2\)

\(\varphi_{a}=\frac{\pm(2 k+1) \pi}{n-m}=\pm \frac{\pi}{3}=\pm 60^{\circ}, 180^{\circ}\)

分离点：

\(\frac{1}{d}+\frac{1}{d+2}+\frac{1}{d+4}=0\)

\(\Rightarrow d_{1}=-0.845, d_{2}=-4.732(\text { 舍 })\)

与虚轴交点：

\(s^{3}+6 s^{2}+8 s+K_{r}=0\)

\(s^{3}\)	1	8
\(s^{2}\)	6	\(K_{r}\)
\(s^{1}\)	\(48-K_{r}\)
\(s^{0}\)	\(K_{r}\)

\(\mathbf{4 8}-\boldsymbol{K}_{r}=\mathbf{0}\)

\(\Rightarrow \boldsymbol{K}_{r}=\mathbf{4 8}, \boldsymbol{s}=\pm \mathbf{j} \mathbf{2} \sqrt{\mathbf{2}}\)

（2）

系统稳定的\(K_{r}<48\)，等幅振荡频率为\(\omega=2 \sqrt{2}\)

6、 设\(G(s)=\frac{K_{r}}{(s+2)^{2}(s+4)}\)，求：

1. 绘制根轨迹图
2. 求系统出现阻尼振荡响应的开环增益的取值范围

解：

（1）

开环零点、极点：\(P_{1}=P_{2}=-2，P_{3}=-4\)

n=3，m=0

n-m=3（3条渐近线）

实轴上的根轨迹段：（-4，-\(\infty\)）

渐近线交点及夹角：

\(\sigma_{a}=\frac{(-2)+(-2)+(-4)}{3}=-\frac{8}{3}\)

$ _{a}=={ \[\begin{array}{l} \frac{\pi}{3}(k=0) \\ \pi \quad(k=1) \\ \frac{5 \pi}{3}(k=2) \end{array}\]

. $

分离点：

\(3S^2 + 16S + 20 = 0\)

\(\Rightarrow d_{1}=-6.333, d_{2}=1(\text { 舍 })\)

此时对应的\(K_{r}\)值为 -43.8

与虚轴的交点：

特征方程

\((s+2)^{2}(s+4)+k_{r}=0\)

\(\Rightarrow s^{3}+8 s^{2}+20 s+16 +k_{r}=0\)

\(s^3\)	1	20
\(s^2\)	8	\(16+K_{r}\)
\(s^1\)	\(\frac{8 \times 20 - (16+K_{r})}{8}\)
\(s^0\)	\(16+K_{r}\)

\(\frac{8 \times 20 - (16+K_{r})}{8}=0\)

\(\Rightarrow K_{r}=144\)，带入\(8s^2 + (16+K_{r}) = 0\) ，解得：

\(s=\pm j 2 \sqrt{5}\)

（2）

7、（5-12）单位反馈系统的开环传递函数为\(G(s)=\frac{K (s+3)}{s(s-1)}\)，试用奈奎斯特判据确定使闭环系统稳定的K值范围

解：

1、绘制图像曲线

起点: \(G(s) \approx \frac{3 k}{-s}, \quad \infty < -270^{\circ}\) ; 终点:$ G(s) , 0 < -90^{}$ ;

交点：分子分母同乘以(s+1),

\(G(s)=\frac{k\left(s^{2}+4 s+3\right)}{s\left(s^{2}-1\right)}\)

\(G(j \omega)=\frac{k\left[\left(3-\omega^{2}\right)+j 4 \omega\right]}{-j \omega\left(\omega^{2}+1\right)}\)

\(G(j \sqrt{3})=-k\)

2、求K值范围

令 z=p-2N=1-2N=0，N 必须为 0.5，由图可见 k>1 即可

8、（5-14）某最小相位系统的开环对数幅频特性如图所示，要求：

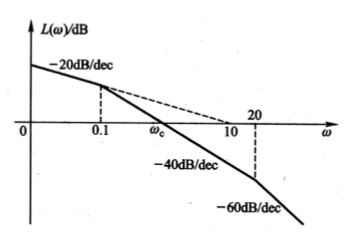
1. 写出系统的开环传递函数
2. 求截止频率及相位裕量\(\gamma\)

解：

（1）由图可得

\(G(s)=\frac{10}{s(10 s+1)(0.05 s+1)}\)

（2）由近似方法求截止频率：

\(G(s) \approx \frac{1}{s^{2}},\) 令 \(\left\vert\frac{1}{s^{2}}\right\vert=1\) 得 \(\omega_{c}=1\)

\(\gamma=180^{\circ}-90^{\circ}-\operatorname{tg}^{-1} 10-\operatorname{tg}^{-1} 0.05=2.848^{\circ}\)

9、二阶系统的结构框图如下，求

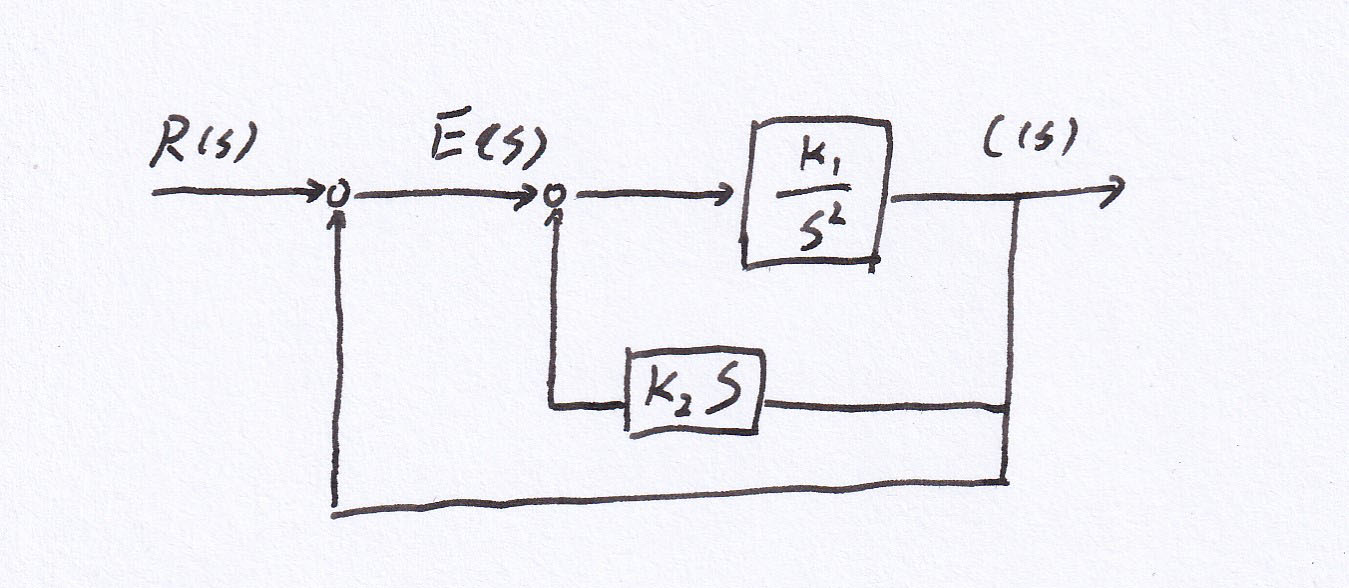
1. 输入信号 r(t) = 1(t) 时，若超调量为20%，调节时间为1.8，求参数\(K_{1}，K_{2}\)
2. 输入信号 r(t) = 2+t 时，求系统的稳态误差

解：

闭环传递函数：

10、系统结构如图所示，求：

1. 用奈氏判据判断系统稳态
2. 当 K < 4 时，求超调量及调节时间
3. 当输入信号为 2(1+t）时，若稳态误差为0.25，求K

解：

\(G(s)=\frac{\frac{k_{1}}{s^{2}}}{1+\frac{k_{1}}{s^{2}} \cdot k_{2}s}=\frac{k_{1}}{s^{2}+k_{1} k_{2} s}\)

\(\phi(s)=\frac{k_{1}}{s^{2}+k_{1} k_{2} s+k_{1}}\)

\(\alpha \%=e^{-\frac{\pi \xi}{\sqrt{1-\xi ^ 2}}} \times 100 \%=20 \%\)